Andere term: Queuing Theory
Doel
De wachtrijtheorie bestudeert en verklaart de verschijnselen die zich voordoen in een wachtrijsysteem waarin bijvoorbeeld een serviceverzoek moet wachten. Elk ingediend verzoek komt eerst in een wachtrij terecht. Zodra er besloten wordt om een verzoek op te pakken, wordt het uit de wachtrij gehaald en afgehandeld.
Een belangrijke stelling uit de wachtrijtheorie is de `stelling van Little’.
Beschrijving
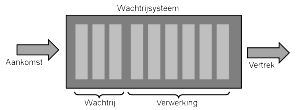
Een wachtrijsysteem is schematisch weergegeven in de onderstaande figuur:
In de wachtrijtheorie spelen de volgende vragen. Hoe snel komen verzoeken aan? Hoe lang staan ze in de wachtrij? Hoe lang wordt er aan een verzoek gewerkt? Welke piekbelasting kan het systeem aan?
Stelling van Little
In 1961 toonde John Little aan dat het verwachte aantal verzoeken in het systeem (L) gelijk is aan het product van hun verwachte aankomstsnelheid (lambda) en hun verwachte verblijftijd (W) in het systeem.

Stelling van Little
Dit geldt voor alle stabiele wachtrijsystemen ongeacht het aantal serviceverzoeken of de variatie in de tussentijd waarmee serviceverzoeken aankomen. Met een stabiel wachtrijsysteem wordt bedoeld dat de snelheid waarmee serviceverzoeken het systeem binnenkomen even groot is als de snelheid waarmee ze het systeem weer verlaten.
Bezettingsgraad
Een belangrijke parameter is de gemiddelde bezettingsgraad van een systeem. Deze bezettingsgraad heeft de verhouding van de hoeveelheid werk die een systeem gemiddeld binnenkomt, tot de maximale hoeveelheid werk die het systeem kan uitvoeren. Is deze bezettingsgraad kleiner dan één, dan is het systeem stabiel, en kan het het binnenkomend werk aan, is de bezettingsgraad groter dan één, dan is het systeem instabiel en zal werk zich opstapelen. Met betrekking tot bijvoorbeeld serviceverzoeken gaat het erom hoe deze serviceverzoeken worden geselecteerd en aangepakt.
Selectie
- FIFO: first in first out
- LIFO: last in first out
- SIRO: service in random order
of - RSS : random selection for service
Gebruik
Een meer bruikbare formulering van de stelling van Little is: de verwachte verblijftijd in het systeem is gelijk aan het aantal serviceverzoeken in het systeem, gedeeld door de gemiddelde vertreksnelheid van een serviceverzoek (omdat het een stabiel systeem is, is de vertreksnelheid gelijk aan de aankomstsnelheid).

Stelling van Little herschreven
Als er 10 serviceverzoeken onderhanden zijn en er wordt gemiddeld 1 verzoek per 7 dagen opgeleverd (gemiddelde vertreksnelheid), dan is de verwachte doorlooptijd (verblijftijd in het systeem) van een serviceverzoek (10 /) 1/7 = 70 dagen.
Om de doorlooptijd te verkorten zijn er in deze formule twee variabelen waarmee gevarieerd kan worden: het onderhanden werk en de opleversnelheid.
Als de opleversnelheid omhoog gaat, daalt de doorlooptijd. Het is mogelijk om de opleversnelheid omhoog te krijgen, maar dan moet vaak het proces ingrijpend aangepast worden (denk aan: beslistrajecten, analyseren, ontwerpen, bouwen, testen). Eventuele “quick wins” leiden niet zelden tot een verminderde kwaliteit, wat op de langere termijn weer meer werk tot gevolg heeft. Stel dat het mogelijk wordt om een verzoek in 6 dagen op te leveren (1 dag minder), dan daalt de doorlooptijd naar (10 / ) 1/6 = 60 dagen.
Het verminderen van de hoeveelheid onderhanden werk leidt ook tot een daling van de doorlooptijd. Hiervoor hoeft het proces in principe niet aangepast te worden. Stel dat het mogelijk is om in plaats van 10 verzoeken maar 6 verzoeken onderhanden te hebben (de 4 minst belangrijke vallen af). In dit geval daalt de doorlooptijd naar (6 /) 1/7 = 42 dagen. In plaats van 70 dagen wachten op een verzoek, hoeft de demandorganisatie nu nog maar 42 dagen te wachten. Dat is al een forse verbetering!

Betere uitleg van Little’s law in IT belevingswereld ben ik nog niet tegengekomen.
Vooral de aanvulling op wat een stabiel systeem betekent, maakt voor mij opeens een hoop duidelijk. In IT is het tempo waarin we vragen doorgaans groter dan het tempo waarin geleverd kan worden. Tegelijkertijd nemen we gelijktijdig meer werk in behandeling dan goed voor ons is. Zie daar de lange levertijden..
Dank